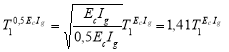Notions of structure

Verification of lateral

displacements of structures

Pre-dimensioning of structural elements

The first step in the design of the structure is to iteratively check the horizontal displacements of the structure. In the case of structures in reinforced concrete frames, this check usually dictates the dimensions of the beams and columns. In elastic calculation, the verification of sags strictly refers to the stiffness of structures to horizontal actions which is dependent on the geometry of the cross-sections of the beams and columns. In this way, the dimensions of the structural elements are finalized and it is then possible to continue with the strength checks without having to repeat the structural calculation. The strength of the structural elements is usually adjusted by changing the reinforcement areas.

Changing the reinforcement areas within certain limits does not significantly change the stiffness of the reinforced concrete elements. In rarer situations, however, it is necessary to modify the sections of the elements. If the dimensions of the structural elements and, implicitly, their stiffness change significantly, it is necessary to repeat the structural calculation because in statically indeterminate structures the distribution of efforts depends on the stiffness of the structural elements.

The verification of lateral movements is done separately for the two main directions of the structure. The first step is to identify, for each design seismic combination, the most deformed frame where the largest level displacements occur (see Combining Action Effects). For this most deformed frame, the values of the absolute displacements are extracted at each level (the displacements of the points compared to the undeformed position) and the relative displacement (the drift) is determined at each level, by differences. The absolute and relative displacements resulting from the structural calculation at the design seismic action for the frame in axis 1 are presented in the following figure. By dividing the relative level displacement by the floor height, the angular drift (expressed in radians) is obtained, which is a measure of the distortion of the columns at that level.

By relation (16) the relative displacement at level 9 was calculated, for example:

According to P100-1/2013, the lateral displacements of the structure are checked at both limit states: ultimate limit state (SLU) and service limit state (SLS).

The displacement verification process is an iterative process. If the analyzed structure does not meet the SLS or SLU verification criteria, it is necessary to increase the gauge of the beams or columns. The structural calculation is redone and the verification conditions are checked again. The calculation is repeated until the verification criteria for both limit states are met. Next, the last iteration of the displacement verification calculation for the analyzed building is presented. In order to meet the displacement verification conditions, it was necessary to increase the size of the corner and marginal posts to 750 mm x 750 mm.

Verification of lateral displacements at the Service Limit State

The verification of lateral movements at the Service Limit State (SLS) is done according to the provisions of Annex E of P100-1/2013. The relative level displacement at SLS is determined by amplifying the relative level displacements resulting from the structural calculation to the design seismic action with the behavior factor, q, and the reduction factor, ν. The displacement values provided by the structural calculation correspond to the action of the design seismic force. This is q times lower than the force to which the structure with elastic behavior would be subjected to the action of the earthquake with an average recurrence interval of 225 years. Therefore, the displacements imposed by this earthquake will be q times greater than those provided by the structural calculation.

On the other hand, the SLS associated earthquake has a shorter average recurrence interval. Thus, the displacement values associated with SLS will be reduced by the factor ν that takes this aspect into account. The value of the factor ν is taken equal to 0.5 according to P100-1/2013.

In the analyzed building, the non-structural walls are made of masonry and are closed in the meshes of the frames. They contribute to the overall rigidity of the structure. In calculating the deformations, their contribution to the overall stiffness of the structure must be taken into account. In this case, the bending stiffness modulus is considered equal to that of the uncracked section:

For example, the relative displacement at level 9 corresponding to SLS is:

The admissible value of the relative level displacement in the situation where there are fragile materials attached to the structure is 0.5% of the level height:

The two values are directly compared and it is observed that the structure fulfills the condition of verification of lateral displacements at the Service Limit State, at level 9.

Similarly, this condition is checked at all levels as shown in the following table and figure. It is observed that the strongest level distortion is recorded at level 3, the verification condition being fulfilled here as well.

If the closing or compartmentalizing walls are made in such a way that they have low stiffness to actions in their plane or if they are arranged in such a way that they do not prevent the lateral deformations of the structure, the bending stiffness of the bar elements in the model is considered equal to that corresponding to the cracked sections of the structural elements. The displacements resulting from the structural calculation are used as such in the SLS checks. Alternatively, it can be chosen that the displacements are determined by structural calculation considering the entire bending stiffnesses of the bars, and then the resulting values of the displacements are multiplied by 2. The permissible value of the relative level displacement is 0.8% of the height of level.

Verification of lateral displacements at the Ultimate Limit State

The calculation of the displacements at the Ultimate Limit State (ULS) is done by amplifying the displacements of the structure actuated by the design seismic force with the behavior factor, q, and with the displacement amplification factor, c (see Annex E, P100-1/2013). Amplification with the behavior factor q is done for the same reason presented when checking lateral displacements at SLS. The factor c makes the transition from the displacements of the structure with elastic response to those of the structure with a response in the inelastic domain. At the earthquake associated with this limit state, the structure has incursions into the inelastic domain.

The displacements of the structure actuated by the design seismic force are determined by considering in the structural calculation the stiffness of the bar-type elements equal to half of the gross bending stiffness of the beams and columns. Even if there are non-structural elements that could contribute to the overall stiffness of the structure, they are degraded during the displacements associated with SLU. Alternatively, the displacement values resulting from the structural calculation under the design seismic force considering the integral bending stiffnesses can be multiplied by 2 to account for the stiffness reduction.

The displacement amplification factor depends on the period of vibration of the structure in the fundamental mode and, implicitly, on the stiffness of the structure. The period of vibration must be determined considering the halved stiffnesses of the structural elements. If the entire stiffnesses of the structural elements were used in the modal calculation, then the vibration period is determined with the following relationship:

In the case of the analyzed structure, the structural calculation was performed considering the unreduced stiffnesses of the structural elements.

As a result, the vibration period of the structure in the fundamental mode in the X direction, T1=0.835 s, must be amplified by 1.41:

This results in an amplification factor, c:

Next, in the verification of displacements in the X direction, the factor c=1.30 is used.

Home